学习数据结构的框架思维
原文是在一个微信公众号里面看到的一篇对于算法概数性的文章,值得反思。文中有些观点值得参考,但是部分观点个人感觉还不是太成熟。数据结构是都是由数组和链表组成,但是就像代码最后落实到机器码就是0和1,美食的原料大部分都原材料只是五谷杂粮等,做法一般有炒、煮、烧、蒸、炸、煎、炖、焖、煲、烩、烤、卤、腌、拌。知道并不代表你就成为大厨了。知其然是成为大神必要不充分的条件。这篇文章从一个较高的抽象层的角度来解释数据结构与算法的一些特性,我也再酝酿一篇算法的术与道的小结,但是总感觉层次还不到。可能就像看山是山,看山不是山,看山还是山的各种层次境界一样吧,
简单说下:就按照排序来说,冒泡,选择,插入,希尔,归并,快排等是术。他们抽象出一些共性来说 冒泡,选择可以说是遍历穷举思想,归并,快排可以说是分治思想。
类似的思想个人小结有:遍历、穷举、分治、局部最优、动态规划、贪婪等吧,暂时有一点想法但是还没想清楚。下面这篇感觉类似,但是比我走的要远一点。但是并不一定说指出才做的不够好就一定要做厨子,你行你上的理论来说。这篇给人一种数据结构跟算法不过如此的感觉,其实不是还是那句话知其然还要知其所以然更要灵活运用。算法的路还很远很长。每一个进步都是人类智慧的结晶。到现在认为数学是最科学的科学。而计算机算法是能让我感兴趣同时也能维持生计的一个很好地结合点。
举个不是很恰当的比喻:算法与数据结构就像做菜手法跟原材料。算法从大的来说就像烹饪手段,数据结构像食材。食材有加工好的,半加工的,或者未加工的。废话不多说了还是转载下。
啰嗦一下:stay foolish!stay hungry!承认自己的局限性,自己的渺小。才能放眼看不一样的风景。
以下原文:
地址:https://mp.weixin.qq.com/s/KVRAPMnVLoyy6p0n3SbMJA
本文是对整个数据结构及算法的总体框架认识,旨在帮助读者自顶向下,从整体到细节,从抽象到具体地看待数据结构。希望通过本文读者能在对数据结构的学习和理解上能有更高层的认识。
先声明一下:首先,这里讲的都是普通的数据结构,咱不是搞算法竞赛的,自学野路子出生,很多厉害的知识我不会,我只会解决常规的问题。另外,以下是我个人的经验的总结,没有哪本书会写这些东西,所以请读者试着理解我的角度,如果不是严重的逻辑错误,没必要纠结于细节问题,因为这篇文章就是希望对数据结构和算法建立一个框架性的认识。相信大家能从这篇文章里学到点东西。
如果你没时间细看,不要错过第四点。
一、数据结构千变万化,但不离其宗
最高层的抽象,数据结构只有两种:数组和链表。
这句话怎么理解,不是还有散列表、栈、队列、堆、树、图等等各种数据结构吗?
我们分析问题,一定要有递归的思想,自顶向下,从抽象到具体。你列出的这么多,都属于「上层建筑」,而数组和链表才是「结构基础」。因为那些多样化的数据结构,究其源头,都是在链表或者数组上的特殊操作,API 不同而已。
比如说「队列」、「栈」这两种数据结构既可以使用链表也可以使用数组实现。用数组实现,就要处理扩容缩容的问题;用链表实现,没有这个问题,但需要更多的空间存储节点指针。
「图」的两种表示方法,邻接表就是链表,邻接矩阵就是二维数组。邻接矩阵判断连通性迅速,并可以进行矩阵运算解决一些问题,但是一般比较耗费空间。邻接表比较节省空间,但是时间上肯定不如邻接矩阵快。
「散列表」就是通过散列函数把键映射到一个大数组里。而且对于解决散列冲突的方法,拉链法需要链表特性,操作简单,但需要空间;线性探查法就需要数组特性,以便连续寻址,省空间,但操作稍微复杂些。
「树」,用数组实现就是「堆」,因为「堆」是一个完全二叉树,用数组存储不需要节点指针,操作也比较简单;用链表实现就是很常见的那种「树」,因为不一定是完全二叉树,所以不适合用数组存储。为此,在这种链表「树」结构之上,又衍生出各种巧妙的设计,比如二叉搜索树、AVL 树、红黑树、区间树、B 树等等,以应对不同的问题。
以上也可以看出,没有完美的数据结构,没有一劳永逸的解决方案。
二、数据结构的操作,无非遍历 + 访问
遍历 + 访问,再具体一点就是:增删查改。
数据结构种类很多,但它们存在的目的都是在不同的应用场景,尽可能高效地增删查改。试问,除此之外还有其他吗?
如何遍历 + 访问?我们仍然从最高层来看,各种数据结构的遍历 + 访问无非两种形式,线性的和非线性的。
线性就是 for/while 为代表,非线性就是递归为代表。无非以下两种框架:
数组遍历框架,典型的线性遍历结构:
void traverse(int[] arr) {
for (int i = 0; i < arr.length; i++) {
// 访问 arr[i]
}
}
二叉树遍历框架,典型的非线性递归遍历结构:
void traverse(TreeNode root) {
traverse(root.left)
traverse(root.right)
}
以上两个框架可以随意改造。
链表遍历框架,兼具线性和非线性遍历结构:
void traverse(ListNode head) {
for (ListNode p = head; p != null; p = p.next) {
// 访问 p.val
}
}
void traverse(ListNode head) {
// 访问 head.val
traverse(head.next)
}
二叉树框架又可以具体扩展为 N 叉树的遍历框架:
void traverse(TreeNode root) {
for (TreeNode child : root.children)
traverse(child)
}
N 叉树的遍历又可以扩展为图的遍历,因为,图就是好几 N 叉棵树的结合体。你说图是可能出现环的?这个很好办,用个布尔数组 visited 做标记就行了,就不贴代码了。
所谓框架,就是说不管具体问题是什么,这些代码都是永远无法脱离的结构,你可以把这个结构作为大纲,根据具体问题在框架上添加代码就行了。
三、为什么算法总是和数据结构同时出现
数据结构是工具,算法是通过合适的工具解决问题的方法。
拿原始人举例,我们学会了数据结构,就像原始人拥有了石刀,石斧等工具。而根据制造工具的工艺不同,石刀又分尖锐的石刀和锯齿状石刀,前者适合打猎,后者适合切割;就像「图」这种数据结构通过不同的实现方法(链表、数组),可以表示为邻接表和邻接矩阵,前者适合处理非稠密图,后者适合处理稠密图。
原始人想要造一栋房子,就要进行规划,石斧砍树,石刀磨尖角等等;就像我们设计算法,发挥数据结构的特性,去解决实际问题。
算法利用数据结构,可以显式利用,比如说前文讲解的 单调栈,就是巧妙地直接利用了栈结构先进后出的特性。稍微高级一点的算法设计思路,就是隐式利用数据结构,比如前文讲过的 回溯算法、动态规划,以及传说中的的分治算法,都在利用树这种结构来解决问题。
但是,无论怎样利用数据结构,多么高大上的算法,其解法都逃不出第二点中相应的框架,是不是?
四、最后总结(重要)
对于一个初学算法的人来说,一定要学会从框架上看问题,而不要纠结于细节问题。
啥叫细节问题?比如说 i 到底应该加到 n 还是加到 n – 1 ?这个数组的大小到底应该开 n 还是 n + 1 ?
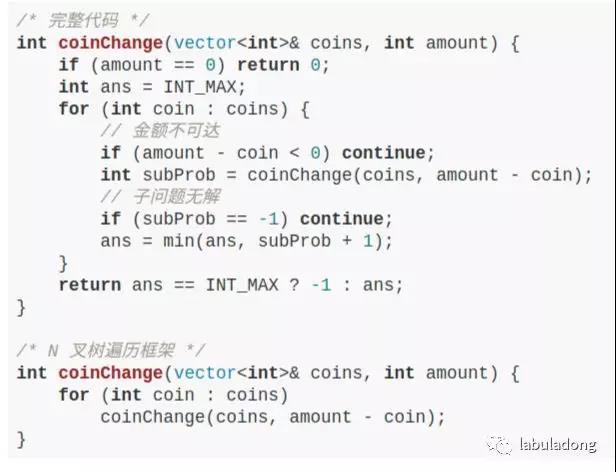
啥叫从框架上看问题?比如说前文 动态规划 中凑零钱的问题,如果你看了一眼代码就自动排除细节问题,直接提取出 N 叉树遍历框架,那么你的框架思维就到位了。
当然,如果细节出错,你得不到正确的答案,但是只要有框架在,你再错也错不到哪去,因为你的方向是对的。
但是,你要是心中没有框架,那么你根本无法解题,给了你答案,你也不会发现这就是个树的遍历问题。
这就是框架的力量,能够保证你在快睡着的时候,依然能写出正确的程序;就算你啥都不会,都能比别人高一个级别。
初学阶段,没到纠结细节的地步。细节出错,可以有各种方法查出来,比如到处打 log,没有找不到的 bug 。
相比之下,别人还束手无策的时候,你已经做出了一个错误的答案;当别人没有框架的指导,被无限细节劝退数据结构的时候,你已经借助框架看穿了数据结构的本质。这不就是一种巨大的成功吗?给你鼓掌。
本文从方向性上面给出了知道,但是路还是要自己走。